代数学II 要約NO10 今日のテーマ シローの定理(2) 定理101 (シローの定理) G の位数がpam (p は素数、m とp とは 互いに素)であるとき、 (1) 位数pa のG の部分群が存在する。 (これをG のpシロー群と04 年度蔵野ゼミ卒業論文 明治大学理工学部数学科 今泉晃広 西祥吾 福岡昌伸 森野拓矢 保村匡亮 渡邉将史 平成17 年2 月18 日 目次 0 序 2 1 アーベル群の基本定理 4 2 代表的な非アーベル群 5 3 半直積 5 4 群の自己同型 8 5 位数がp またはp2 の群 10 6 位数が2p の群の分類(p は奇素数) 10 7 シロー部分群群論問題集 2 群準同型 21 群準同型 1 G, H を群とする。 写像f G → H が群準同型であることの定義を答えよ。 2 f G → H を群準同型とする。 (1) f(1G) = 1H であることを示せ。 (2) a ∈ G に対してf(a 1) = f(a) 1 であることを示せ。 3 f G → H を群準同型とする。a ∈ G は位数o(a) が有限の元

4 群作用 ノリの悪い日記
シロー の 定理
シロー の 定理-5に おいて全て決定する.また,一般のpにおいてのpSylow部分群の構造を考察する. 14 参考 同研究室の菅亮輔氏がSylow 部分群と正多面体の対称性の関係について研究している131 シローの定理 51 14 交換子, 可解性, 補足 55 141 交換子, 交換子群 55



Www2 Tsuda Ac Jp
この定理はSylowの定理の証明によく用いますので,覚えておいてください. 内部自己同型 群 \(G\) があって次の写像を考えます. $$G\times G\ni (g,x)\longmapsto i_g(x)=gxg^{1}\in G$$ この写像は $$i_{gh}(x)=(gh)x(gh)^{1}=g(hxh^{1})g=i_g(i_h(x)) \\ {i_e(x)=exe^{1}=x}$$シローの定理証明&応用 この記事では, シローの定理(Sylow theorems)の証明&応用について解説します。 シローの定理の証明 シローの第1定理 定理 $p$ が素数で, $G$ が $p^a$ で割り切れるならば, $G$ は位数 $p^a$ の部分群をもつ 証明 証明3.シローの定理 31.群の集合への作用 本節では、シローの定理の準備として、"群の集合への作用"という概念を説明する。これはそれ自体独立し た概念であり、応用範囲が広くその具体的事例のひとつがシローの定理である。 群の集合への作用
シローおよびフロベニウスの 定理を結ぶゼータ関数 吉田知行 (Tomoyuki YOSHIDA 概略 北大・理) 有限群における部分群の個数や、その群上の方程式の解の個数は古くから研究されてきた。Sylowの定理 黒木玄 07年10月16日 定義1 G は有限群であり, p は素数であり, G の位数がpem (m はp で割り切れない) と 表わされてるとする このときG の位数pe の部分群をG のSylow p 部分群と呼ぶ 例2 体K の元を成分に持つn 次上三角行列で対角成分がすべて1 であるもの全体のシローの定理 著者名: 佐藤隆夫 価格 ¥2,640 (本体¥2,400) 近代科学社 (18/08発売) ポイント 24pt (実際に付与されるポイントはお支払い画面でご確認下さい) ISBN: ツイート 発行形態:書籍 ファイル: PDF形式 / 193MB iPhone、iPod touch、iPad
準同型定理より Im(f)≃ Q/Ker(f) となるため、ラグランジュの定理よりIm(f)の位数はqの約数になります。よって1かqです 一方で、Im(f)はAut(P)の部分群なのでその位数はp1の約数となります。qはp1を割りきらなかったので Im(f)=1 ∴Im(f)={1} となります ナイス! 質問者からのお礼コメント なるほど数学、とくに有限群論において、シローの定理 (英 Sylow theorems) は、ノルウェーの数学者ルートヴィヒ・シロー (Ludwig Sylow) (1872) にちなんで名づけられている定理の集まりであり、与えられた有限群がもつ固定された位数の部分群の個数についての詳細な情報を与える。Sylow の定理は次の定理です. $ \newcommand{\Syl}{\operatorname{Syl}} $ 任意の有限群$G$について, その位数が素数$p$,$p$に互いに素な正数$m$,そして非負整数$n$によって $G=p^{n}m$と表されるとする.




書泉グランデmath 営業時間11時 時 現代数学社数学書フェア 開催中 群論への招待 永田雅宜 置換群を早期に扱い 置換群の例をイメージに持ちながら いろいろな定義を理解していけるよう構成 sylow シロー の定理やアーベル群の指標など




電波 こういうのシローの定理使うと吹き飛ぶよね
シローの定理 適用例 巡回群の位数位数 n の群は巡回群に限るような正の整数 n がある。たとえば n = 15 がそのような数であることがシローの定理を用いることでわかる。ここで n3 5 かつ シローの定理とは シローの定理とはシローさんが発見した有限群論の定理たちの総称です その中で僕が一番好きなのは $p_i\in \mathbb{P}$とする$ G=p_{1}^{e_1}p_{2}^{e_2}\cdots p_{k}^{e_k}$であるとき 位数$p_{i}^{e_i}$である部分群が存在する という存在定理ですローの定理のあたりで時間的に厳しくなります シローの定理の後で何をする か,ということは個人的な好みの差があると思いますが,私だったら具体例と して位数12 の群の分類をします そのために生成元と関係式が必要で,時間が あったら有限アーベル群をやるというのが,個人的な方針




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon




An Elementary Proof That A Simple Group Of Order 360 Is Isomorphism To A 6 Semantic Scholar
定理(Sylow の定理) (1) G のpSylow 部分群は存在する (2) pSylow 部分群の個数k(p) はk(p) 1 (mod p) かつk(p)jjGj を満たす (3) 任意のp 部分群H ˆ G に対して, あるg 2 G が存在してgHg 1 はpSylow 部分群に含まれる 特に pSylow 部分群はすべて共役である 系 pSylow 部分群が1 つしかない場合, それは正規部分群にシロー部分群とするとき,G7 ∩G11 = {eG} であるから, ♯ ( G\ ( G 7 ∩G 11 )) = 77 − 7 − 111 = 60 である.この60 個からなる集合は位数が77 の集合である.60 個の元のうち任意に g をひとつラグランジュの定理の直感的な証明 有限群gの部分群をhとするとき、 gの位数はhの位数で割り切れる いよいよラグランジュの定理! まず 群マシンで、 直感的な証明をするわよ。 ゆえに 0 8 9 7 6 5 4 3 2 1 10 11 8 5 2 7 11 4 1 10 0 9 6 3 = #g = #(h★0) #(h★1




暗号理論入門 暗号アルゴリズム 署名と認証 その数学的基礎 Buyee日本代购服务 在honto购物 Bot Online




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon
群論(シローの定理あたりまで) 対象:2,3回生 抽象的な定義・理論にまず慣れるという意味では,とにかく平易な解説と簡単な例がいくつも書いてあるものが良いでしょう.その意味では, (1) 新妻 弘・木村 哲三著,「群・環・体入門」,共立出版 シローの定理から位数 G p = q n(n − 1)/2 のシロー p部分群 U が存在する。たとえば n = 3 のとき = {() ,,}ベルの定理 (局所的な隠れた変数の理論は量子力学と矛盾する) l→ ~c ~(l∩ ~c) 結論~l (c)eprの 議論とベルの定理の両方を受け入れるならば,局 所性の前提 lは放棄しなければならないし かしながら,局所性の原理の破綻が,遠 隔作 用の実在性を意味するのであれば,量子力学と相対性理論との




代数学1 群論入門 日本評論社




Hiroki S Papa の出品した商品 メルカリ
Sylowの定理 Sylow p 部分群に対して,次 4 つが成り立つ. (1) 有限群 は,任意の素数 に対して, Sylow p 部分群を持つ. (2) 有限群 の p 部分群はある Sylow p 部分群に含まれる. (3) Sylow p 部分群は互いに共役である. (4) Sylow p 部分群の個数を とすると, (2) 有限群 の p 部分群はある Sylow p 部分群に含まれる. 代数学の基本定理 は,このような 複素数 係数の 多項式 は2次以外の場合でも (具体的な根が求められるかどうかは別として) 複素数 の範囲で根を持つという主張です. その完全な証明は18世紀に ガウス が初めて与えたといわれています. この本はそのシローの定理 の用例・例文集 これの逆の主張の一部はシローの定理が与えてくれる。シローの定理とともに用いて有限単純群の存在性に関するある種の数的な結果を得るために利用できる。シローの定理はラグランジュの定理の部分的な逆を主張する。




4 群作用 ノリの悪い日記




巡回群 Wikiwand
G の位数6 の部分群は定理31 からS3 と同型である.H ⊂ G を位数 6 の部分群とする.H は{1,2,3,4} に作用して,一つの軌道をω とする と,固定部分群の位数は1,2,3, 又は6 だから♯ω = 3,2 又は1 である. H がG の3Sylow 部分群 M4 (M4 の周りの60 度回転で生成された)(4) シローの定理を用いて、簡単な群の構造を決定できる。 (5) 巡回群、対称群、二面体群などの群に対し、(1) ~(4) の内容を適用できる。 履修上の注意 Course notes prerequisites 予習、復習を十分行った上で出席すること。 教科書として次の書籍を利用する:シローの定理は,群の位数と部分群に関する,次のような定理です. theorem 群 の位数が,素数 によって と,一意的に素因数分解されるとき,位数が となる部分群が少なくとも一つは存在する.




19年2月9日 可換体論 永田雅宜 著 私のお気に入りの書籍 シローの定理 に感動 ガロア理論 や 正17 角形の作図可能 など つれづれなるままの数学 算数 素数gpsの周辺 Iphoneとandroid 366 Aps




Pdf The Principal 2 Blocks Of Finite Groups With Abelian Sylow 2 Subgroups
シローの定理の問題です。 試験が近いので、助けてください! pとqは、素数でp>qとする。 もし、p≡1 (mod q)でないとき、位数pqのどのような群も巡回群であることを示してください。 数学 帰納法を用いたシローの定理の証明について: 下記の資料のp54~55に 帰納法を用いたシローの定理(シロー部分群の存在)が記載されています.(定理153) http//wwwシローの定理 佐藤隆夫(数学) 本の購入は楽天ブックスで。全品送料無料!購入毎に「楽天ポイント」が貯まってお得!みんなのレビュー・感想も満載。シローの定理によりk 1 はp の倍数であることに注目すると、上の こととあわせてpシロー群の数について強い制限がつくことが分かる。 次の二つの補題も位数が低い群を調べる際には有効である。 補題112 群G の素数位数の部分群P1;P2 があるとき、P1 = P2 ま たはP1 \P2 = feg のどちらかが成り立つ




日本の定理 Owlapps




講談社サイエンティフィク 18年4月 新刊紹介 その1 今度こそわかるガロア理論 芳沢光雄 著 Www Kspub Co Jp Book Detail Html 置換群を専門とする著者による 丁寧な解説 群 環 体の基礎から 方程式の可解性まで これぞ 芳沢流
可解群とシローの定理,そして今後遭遇するであろう(興味深い)群論の定理をいくつか紹介する. Fact と書いてあるものについては,証明はしないが標準的な(あるいはより進んだ)群論の教科 書に載っている内容なので,興味のある人は調べてみたり,自分で証明を考えてみる事をおすすめ し41 シローの定理 35 5 群の直積 39 51 外部直積 39 の位数が であるときを考える.このとき,位数 の の部分群( 部分群という)は必ず存在する(定理4).Sylowの定理(定理7)は,位数が の部分群(このような部分群を の Sylow群という)についての定理である.Sylowの定理は有限群を考える上で基本的なものである. このレポートでは,Sylowの定理を両側分解の考え方で証明したあと,Sylowの定理の応用とし



シローの定理 大学数学スポットライト シリーズ 佐藤隆夫 全集 双書 通販 Lineポイント最大0 5 Get Lineショッピング




群論 シロー部分群の共役関係 スライド版 龍孫江 りゅうそんこう 可換環論botオペレーター Note
10 群論3 (群作用, Sylow の定理) 101 群作用と軌道分解 問題101 (1) ex = x よりe 2 Gx 任意のg 2 Gx について, g 1x = g 1(gx) = (g 1g)x = ex = x よりg 1 2 G x またg1;g2 2 Gx ならg1(g2x) = g1x = x なのでg1g2 2 Gx 以上よりGx は部分群 (2) x = g 1y に注意する 実際, g 1y = g 1(gxシローの定理 発売日:15年4月10日 定価:本体2,400円+税 紀伊國屋書店 で注文 アマゾン で注文 群論の古典! シローの定理からP3:3-Sylow部分群 s3:P3の個数 P2:2-Sylow部分群 s2:P2の個数 とすると、シローの定理からs3=1、s2=1,3となり、 ということは分かったのですが、 教えていただけませんですか? 通報する この質問への回答は締め切られました。 質問の本文を隠す A 回答 (1件) ベストアンサー




群論 シロー部分群の数 Youtube




シローの定理 大学数学スポットライトシリーズ1 佐藤 隆夫 楽天kobo 日本




代数学 26 シローの定理 Youtube




シローの定理 Wikipedia




シローの定理 Wikipedia



Icu Hsuzuki Github Io




Algebra I Lecture Note
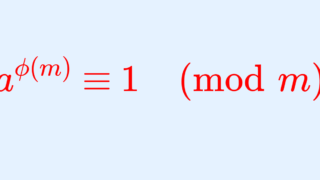



P 1 1 ウィルソンの定理とその4通りの証明 数学の景色




代数学 1 群論入門 メルカリ




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon



環論 シローの定理 画像の命題kが有限体なら K は Yahoo 知恵袋




シローの定理 大学数学スポットライトシリーズ1 佐藤 隆夫 楽天kobo 日本



群論への30講 17講くらいまで読んだ感想 乱文 Nobishino 勉強ブログ




シローの定理とその応用 7931のあたまんなか




つれづれなるままの数学 算数 素数gpsの周辺 Iphoneとandroid 366 Aps 19年02月




シローの定理 数学ノート置き場




シローの定理とその応用 7931のあたまんなか




ガロア理論とシローの定理でℂ代数閉体を示す 数学雑感




シローの定理の通販 佐藤 隆夫 矢部 博 紙の本 Honto本の通販ストア




P 1 1 ウィルソンの定理とその4通りの証明 数学の景色




シローの定理 佐藤隆夫の本 情報誌 Tsutaya ツタヤ
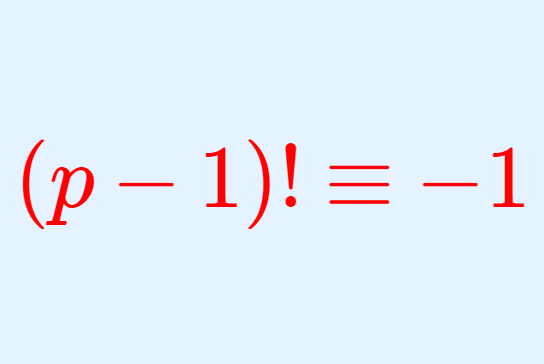



P 1 1 ウィルソンの定理とその4通りの証明 数学の景色




Qun Lun Qun Beru Qun R Bikkuky Bu Z Ori Rumi Qun Dui Ch Ng Qun Qun Zuo Yong Kokuset Qun Er Mian T Qun Qun Lunno Yong Y Bu F N



Proof Sample Of Hierarchical Style



Imetrics Co Jp



Www2 Tsuda Ac Jp




龍孫江の数学日誌 Sylowの定理




Sylow の定理から Cauchy の定理を示したいのですが 次のような証明で良いのでしょうか G を位数が P の倍数である群とする G の P シロー部分群において単位元でなく位数が P E E Gt 0 の元 X をとる このとき X P E 1 は位数 P の元である マシュマロ




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon



レポート代行 Com




シローの定理 べっこう色の記録




ふわラテ 数学セミナー 21年10月号 特集 楕円函数の味わい です 他にも バナッハ空間 シローの定理 ケーリーグラフなど盛りだくさん 原 啓介先生の書棚探訪も一読の価値あり 読書の秋 本のベスト10 で今売れ筋の本も要チェック 面白い




19年2月9日 可換体論 永田雅宜 著 私のお気に入りの書籍 シローの定理 に感動 ガロア理論 や 正17 角形の作図可能 など つれづれなるままの数学 算数 素数gpsの周辺 Iphoneとandroid 366 Aps




Algebra I Lecture Note




Sylow S Theorem For Association Schemes Codes Lattices Vertex Operator Algebras And Finite Groups




やきにく 今年の副ゼミが無事に終わった 雪江明彦 群論入門 1ページから90ページまでほぼ全ての演習問題 証明含めてカバーした 発表時間は90分 13回 1170分 約時間 準備時間はその2倍の40時間くらいかな 来年はシローの定理やガロア理論まで



シローの定理 数学ノート置き場




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon



シローの定理 大学数学スポットライト シリーズ 佐藤隆夫 全集 双書 Hmv Books Online Yahoo 店 通販 Yahoo ショッピング




おはようございmathのtwitterイラスト検索結果




シローの定理 佐藤隆夫の本 情報誌 Tsutaya ツタヤ




10 シローの定理



シローの定理 物理のかぎしっぽ




可解群 Wikiwand




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon




シローの定理で朝食を 妄形少女と秘密のクロヲゼット




シローの定理 通販 セブンネットショッピング オムニ7




Pdf Sylow S Theorem For Association Schemes



Www1 Ezbbs Net




Introduction Of Introduction To Group Theory




シローの定理とは サイエンスの人気 最新記事を集めました はてな




シローの定理 Wikipedia




群論 シロー部分群は存在します Youtube




シローの定理 数学ノート置き場



シローの定理からコーシーの定理を 導く証明について以下のように Yahoo 知恵袋




シローの定理 大学数学スポットライトシリーズ1 佐藤 隆夫 楽天kobo 日本




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon



レポート代行 Com



Math Keio Ac Jp
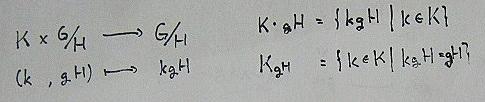



シローの定理とは サイエンスの人気 最新記事を集めました はてな




Sylow S Theorem For Association Schemes Codes Lattices Vertex Operator Algebras And Finite Groups




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon




Algebra I Lecture Note




シローの定理 べっこう色の記録




Algebra I Lecture Note



シローの定理 通販 Lineポイント最大2 0 Get Lineショッピング




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon




群論 正規部分群のシロー部分群 龍孫江 りゅうそんこう 可換環論botオペレーター Note




書泉グランデmath 営業時間11時 時 En Twitter 書泉グランデがすすめる大学数学はじめの一歩フェア 開催中 シローの定理 佐藤隆夫 著 近代科学社 シローの定理 にスポットをあて より深い理解を目指して学ぶことができる 章末には 演習問題の詳細
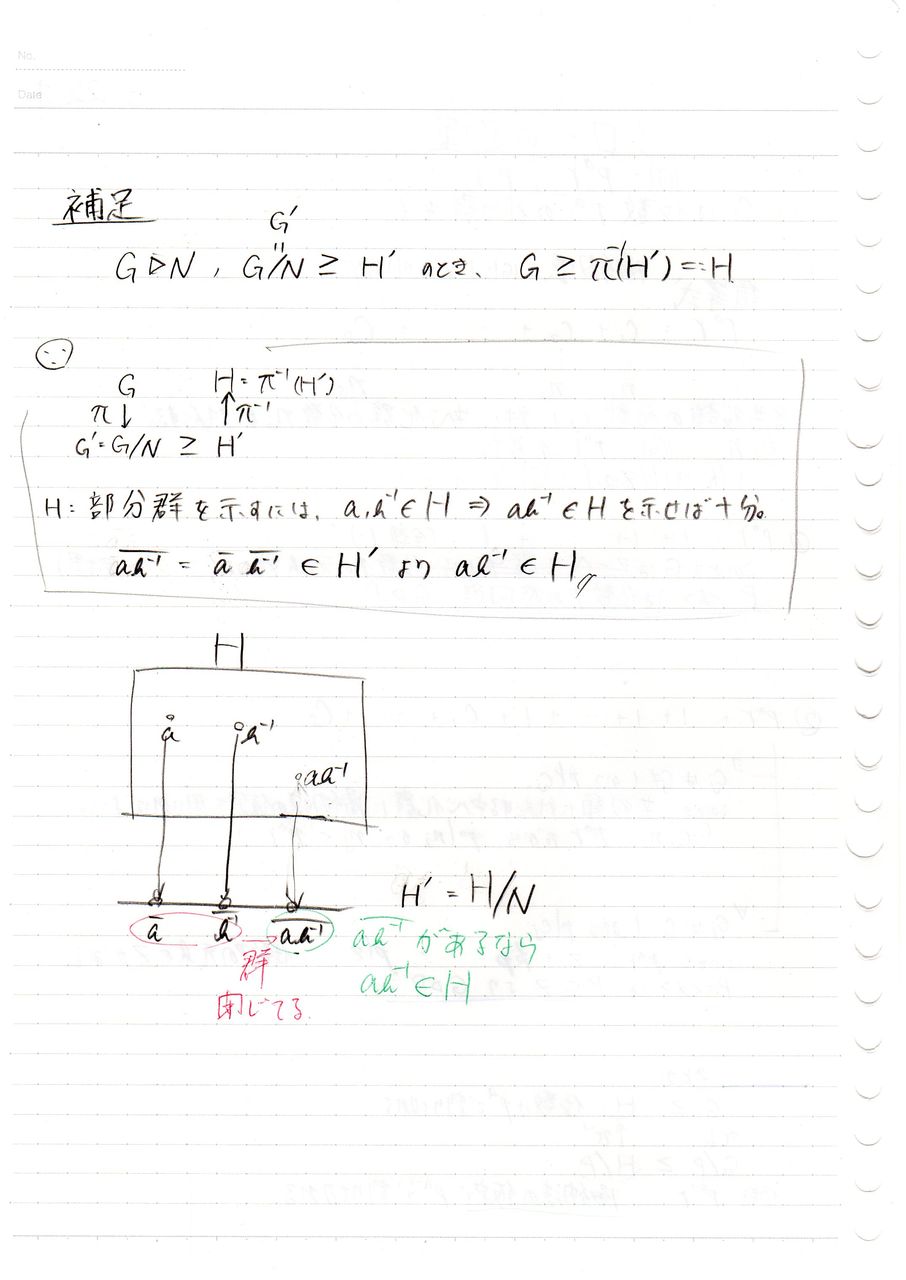



シローの定理 数学ノート置き場




ラグランジュの定理 群論 Wikipedia




書籍紹介 代数入門 堀田良之 著 数学




シローの定理とは サイエンスの人気 最新記事を集めました はてな




10 シローの定理



代数学の基本定理の シローの定理やガロア理論を用いた 代数的証明 ぱいおつ日記




シローの定理の偉大さ Qiita



シローの定理 べっこう色の記録



書籍 シローの定理 大学数学スポットライト シリーズ 佐藤隆夫 著 Neobk 通販 Lineポイント最大get Lineショッピング



レポート代行 Com




シローの定理 佐藤隆夫の本 情報誌 Tsutaya ツタヤ




シローの定理 数学ノート置き場




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon




シローの定理 4 1に取り掛かる と言ってもこれを書いてる時点で終わってるんだけどね Kyutamのブログ




シローの定理 4 1に取り掛かる と言ってもこれを書いてる時点で終わってるんだけどね Kyutamのブログ


